Question

What is the greatest integer that always divides the difference of the squares of any two different positive odd integers?

Answer 1

The greatest integer is 8.

Explanation:

Odd positive integers are positively directed numbers that can not be divided into to equal values without a remainder. Examples are: 1, 3, 5, 7, 9 etc.

Given the following positive odd integers:

i. 9 and 3

`9^(2)` -
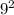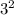`3^(2)` = 81 - 9

= 72

ii. 3 and 1,

`3^(2)` -
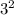`1^(2)` = 9 - 1

= 8

iii. 7 and 5

`7^(2)` -
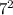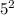`5^(2)` = 49 - 25

= 24

iv. 21 and 13

`21^(2)` -
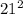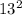`13^(2)` = 441 - 169

= 272

Therefore, it can be observed that the greatest integer that always divides the difference is 8.