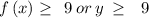Question

The function f(x) = x is translated using the rule (x, y) - (x - 6, y + 9) to create A(x).

Which expression describes the range of A(x)?
Oy2-9
Oy6
Oy26
O y29

Answer 1

d on 3dge

Explanation:

genius

Answer 2

It seems the correct function you need to mention is f(x) = sqrt x

so, I am assuming
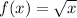`f(x) = √(x)` and will solve the question based on it.

Answer:

Check the explanation

Explanation:

Given the function

`f(x) = √(x)`

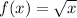
As the function is translated according to the rule

• (x, y) → (x - 6, y + 9)

Translation of the function
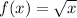`f(x) = √(x)` 6 units to the left will bring the function

`g(x) = √(x+6)`

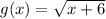
Translation of the function
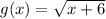`g(x) = √(x+6)` 9 units up will bring the function

`A\left(x\right)=√(x+6)+9`

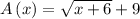
Determining the range of
`A\left(x\right)=√(x+6)+9`

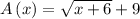
• As we know that the range is the set of dependent values for which the function is defined.

`\mathrm{The\:range\:of\:an\:radical\:function\:of\:the\:form}\:c√(ax+b)+k\:\mathrm{is}\:\:f\left(x\right)\ge \:k`

`k=9`

`f\left(x\right)\ge \:9`

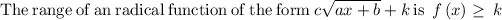
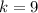
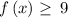
so

`\mathrm{Range\:of\:}√(x+6)+9:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)\ge \:9\:\\ \:\mathrm{Interval\:Notation:}&\:[9,\:\infty \:)\end{bmatrix}`

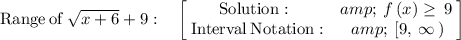
Therefore, the expression describes the range of A(x) will be:

`f\left(x\right)\ge \:\:9\:or\:y\:\ge \:\:\:9`