Question

Consider the following sequence of numbers.

3,-9,27,-81,...
I need common ratio & sum of 1st five terms

Answer 1

Please check the explanation

Explanation:

Given the sequence

`3,-9,27,-81,...`

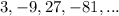
A geometric sequence has a constant ratio and is defined by

`a_n=a_0\cdot r^(n-1)`

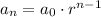
Computing the ratios of all the adjacent terms

`r=(a_n+1)/(a_n)`

`(-9)/(3)=-3,\:\quad (27)/(-9)=-3,\:\quad (-81)/(27)=-3`

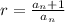
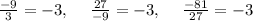
The ratio of all the adjacent terms is the same and equal to

`r=-3`

Therefore, the common ratio is:

• r = -3

Determining the sum of 1st five terms

As the first element is

`a_1=3`

`r=-3`

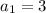
Geometric sequence sum formula is given by

`a_1(1-r^n)/(1-r)`

Plugin the values

`n=5,\:\spacea_1=3,\:\spacer=-3`

`a_1(1-r^n)/(1-r)=3\cdot \:(1-\left(-3\right)^5)/(1-\left(-3\right))`

`=3\cdot (1-\left(-3\right)^5)/(1+3)`

`=(\left(1-\left(-3\right)^5\right)\cdot \:3)/(1+3)`

`=(732)/(1+3)` ∵

`=(732)/(4)`

`=183`

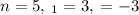
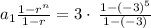
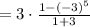
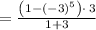
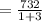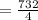
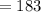
Therefore, the sum of the first five terms of the sequence is: 183