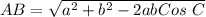Answer:
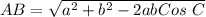
Explanation:
Given:
The above triangle
Required
Solve for AB in terms of a, b and angle C
Considering right angled triangle BOC where O is the point between b-x and x
From BOC, we have that:
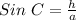
Make h the subject:
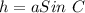
Also, in BOC (Using Pythagoras)
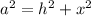
Make
 the subject
the subject

Substitute
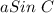 for h
for h
 becomes
becomes
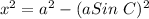
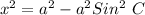
Factorize

In trigonometry:
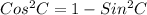
So, we have that:
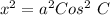
Take square roots of both sides
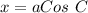
In triangle BOA, applying Pythagoras theorem, we have that:
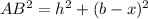
Open bracket
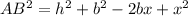
Substitute
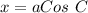 and
and
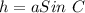 in
in
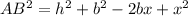
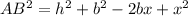

Open Bracket

Reorder
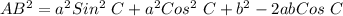
Factorize:
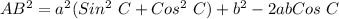
In trigonometry:

So, we have that:
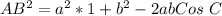
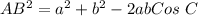
Take square roots of both sides