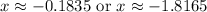Answer:
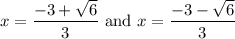
Or, by approximating:
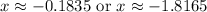
Explanation:
Let’s convert this to standard form. We have:
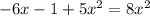
Subtract 5x² from both sides:
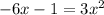
And add 6x and 1 to both sides:
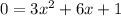
This is not factorable. So, we will need to use the quadratic formula.
The quadratic formula for a quadratic in standard form is given by:
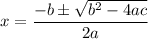
In this case, a=3; b=6, and c=1.
Substitute appropriately:
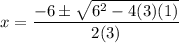
Simplify:
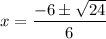
We can simplify the square root:
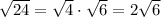
Hence:
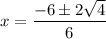
Simplify:
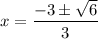
Hence, we will have two solutions:
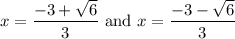
Approximating them, we can see that our solutions are approximately: