Question

Please help: If the area of a rectangular picture of a stamp is 81 times greater than the actual stamp's area, and the stamp has a length of 4/3". what is the length of the stamp's picture?​

I know the answer is 12 inches but not sure how to get there so pls explain

Answer 1

12 inches.

Explanation:

We know that the length of the stamp is 4/3 inches.

Let the width be x inches.

Then the area of the actual stamp is:

`(4)/(3)x\text{ inches}^2`

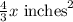
We know that the rectangular picture of the stamp is 81 times greater than the actual stamp’s area. Therefore, the area of the picture is 81 times the above. So:

`81((4)/(3)x)\text{ inches}^2`

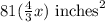
So, the area of the rectangular picture is the area of the actual stamp multiplied by a scale factor k.

When we use the scale factor to scale area, we need to square it. Hence, the area of the actual stamp times the scale factor squared is equal to the area of the rectangular picture. Therefore:

`(4)/(3)x(k^2)=81((4)/(3)x)`

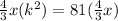
Let’s solve for the scale factor. Divide both sides by 4/3(x). Hence:

`k^2=81`

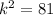
Take the square root of both sides:

`k=9`

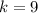
So, the scale factor from the actual stamp to the picture is 9.

So, the actual stamp has a length of 4/3.

Then ThThe length of the stamp’s picture will be:

`(4)/(3)k`

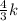
Substitute 9 in for k to get:

`=(4)/(3)(9)=12`

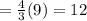
So, the length of the stamp’s picture is 12 inches.