Question

In rectangle ABCD, diagonals AC and BD intersect at E. If AE=3x-28 and DE=.5x+12, find the length of AC.

Answer 1

Given:

In rectangle ABCD, diagonals AC and BD intersect at E, AE=3x-28 and DE=.5x+12.

To find:

The length of AC.

Solution:

We know that, diagonals of a rectangle are equal and they bisect each other.

In rectangle ABCD, diagonals AC and BD intersect at E, so

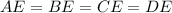`AE=BE=CE=DE` ...(i)

Taking
`AE=DE`, we get

`3x-28=0.5x+12`

`3x-0.5x=28+12`

`2.5x=40`

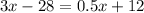
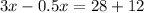
Divide both sides by 2.5.

`x=(40)/(2.5)`

`x=16`

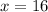
Now,

`AE=3x-28`

`AE=3(16)-28`

`AE=48-28`

`AE=20`

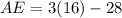
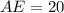
Using segment addition property,

`AC=AE+CE`

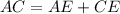
`AC=AE+AE` [Using (i)]

`AC=20+20`

`AC=40`

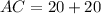
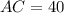
Therefore, the length of AC is 40 units.