Answer:
The distance from vertex B to the midpoint of AC is 3.
Explanation:
From Linear Algebra we understand that location of the midpoint of AC is determined by the following formula:
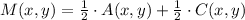 (1)
(1)
Where:
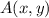 ,
,
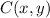 - Locations of vertices A and C regarding origin, dimensionless.
- Locations of vertices A and C regarding origin, dimensionless.
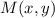 - Location of the midpoint regarding origin, dimensionless.
- Location of the midpoint regarding origin, dimensionless.
If we know that
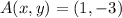 and
and
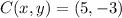 , then the midpoint of AC is:
, then the midpoint of AC is:
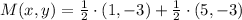
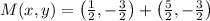
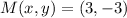
Lastly, the distance from vertex B to the midpoint of AC is calculated from the Pythagorean Theorem:
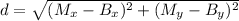 (2)
(2)
If we know that
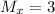 ,
,
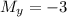 ,
,
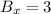 and
and
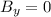 , then the distance is:
, then the distance is:
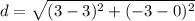

The distance from vertex B to the midpoint of AC is 3.