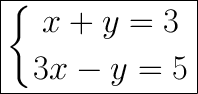
We can solve this problem by testing the solution against each system of equations. We'll do this by substituting the point into each equation for each system.
System 1 -
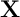
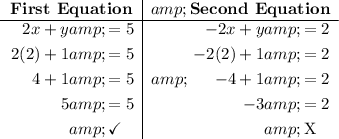
System 2 -

System 3 -
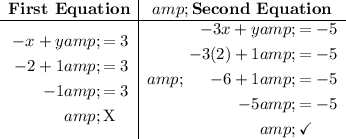
System 4 -


Since both equations in the final system are true when solved with
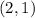 , the answer is the last system.
, the answer is the last system.