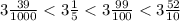Question

I don't understand this question, help me, someone, please

Answer 1

Arranging the terms from least to greatest:

`(3039)/(1000)<(3200)/(1000)<(3990)/(1000)<(8200)/(1000)`

Now actual terms arranged from least to greatest will be:

`3(39)/(1000)<3(1)/(5) <3(99)/(100)<3(52)/(10)`

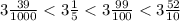
Explanation:

We need to arrange the weights
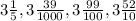`3(1)/(5) ,3(39)/(1000),3(99)/(100),3(52)/(10)` from least to greatest.

To arrange them in least to greatest we need to convert them into improper fractions and then make their denominators same.

`3(1)/(5)=(16)/(5) \\3(39)/(1000)=(3039)/(1000) \\3(99)/(100)=(399)/(100) \\3(52)/(10)=(82)/(10)`

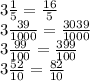
Now, Making their denominator same by taking LCM of 5,1000,100 and 10

The LCM is 1000

Now the fractions will become:

`(16)/(5)=(16*200)/(5*200)=(3200)/(1000)`

`(399)/(100)=(399*10)/(100*10)=(3990)/(1000)`

`(82)/(10)=(82*100)/(10*100)=(8200)/(1000)`

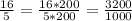
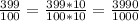
Now we have fractions:
`(3200)/(1000),(3990)/(1000),(8200)/(1000),(3039)/(1000)`

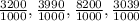
Now the smallest term will be one having smallest numerator

Arranging the terms from least to greatest:

`(3039)/(1000)<(3200)/(1000)<(3990)/(1000)<(8200)/(1000)`

Now actual terms arranged from least to greatest will be:

`3(39)/(1000)<3(1)/(5) <3(99)/(100)<3(52)/(10)`