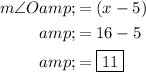Since we know that all angles in a triangle add up to
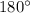 , we can solve for
, we can solve for
 and substitute it back into
and substitute it back into
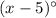 to find
to find
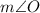 .
.
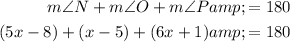
Remove the parentheses and combine like terms.
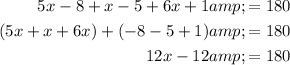
Add
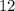 to both sides of the equation.
to both sides of the equation.
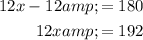
Divide both sides of the equation by
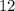 .
.
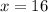
Now that we have the value of
 , we can substitute it back into
, we can substitute it back into
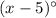 to find
to find
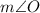 .
.