Question

(ANSWER FOR FREE BRAINPOINTS!) (FIRST TO ANSWER GETS BAINLIEST) The local park has a rectangular swimming pool that measures 40 yards in length and 15 yards in width. The community is planning to build a smaller swimming pool that is similar to the current pool. 40 yards, 15 yards, 24 yards. If the length of the new smaller pool will be 24 yards, what will be the width of the smaller pool in yards?

Answer 1

9 yards

Explanation:

Since both pools are similar, therefore the ratio of their length and width would be equal. That is:

Length of the current swimming pool : length of the new swimming pool = width of the current swimming pool : width of the new swimming pool

Thus, we can set up a proportion as shown below:

Let the width of the new swimming pool be x.

40 : 24 = 15 : x

`(40)/(24) = (15)/(x)`

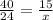
Cross multiply

`40*x = 15*24`

`40x = 360`

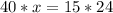
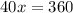
Divide both sides by 40

`x = (360)/(40)`

`x = 9`

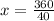
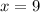
The width of the new swimming that is smaller would be 9 yards.