Question

Consider the following Theorem: If A B and C are angles of an oblique, non-right, triangle, then Tan(A) + Tan(B) + Tan(C) = Tan(A)Tan(B)Tan(C). Choose values for A, B, and C, then verify that the conclusion is true for your specific values.

Show all of your work and attach it with the answer.

Answer 1

tan A + tan B + tan C = tan A tan B tan C

Explanation:

Explanation:-

proof:-

Given A B and C are angles of an oblique, non-right, triangle

we know that A+B+C = 180

A+B = 180 - C

Apply ' tan' on both sides , we get

Tan(A+B) = Tan ( 180 - C)

`(tan A+ tan B)/(1-tanA tan B) = tan( 180 -C)`

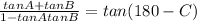
tan A + tan B = - tan(180- C) ( 1 - tan A tan B )

tan A + tan B = - tan C ( 1 - tan A tan B )

tan A + tan B = - tan C + tan A tan B tan C

tan A + tan B + tan C = tan A tan B tan C