Triangle M was dilated by a scale factor of 1.2 to form triangle M. How does the area of triangle M' relate to the area of triangle M? A- The area of triangle M'is 0.6…

Question

asked Sep 15, 2021 104k views

2 Answers

Kote · Answer 1 · 2021-09-19T09:40:53+0000

Answer:

The area of triangle M is 1.44 times the area of triangle M.

Explanation:

From Geometry we remember that the area formula of the triangle is:

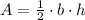$A = (1)/(2)\cdot b\cdot h$ (1)

Where:

- Base of the triangle, dimensionless.

- Height of the triangle, dimensionless.

- Area of the triangle, dimensionless.

The dillation of the triangle by a scale factor means that:

$A' = (1)/(2)\cdot b'\cdot h'$ (2)

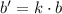$b' = k\cdot b$ (3)

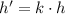$h' = k\cdot h$ (4)

Where:

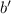- Dilated base of the triangle, dimensionless.

- Dilated height of the triangle, dimensionless.

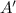- Dilated area of the triangle, dimensionless.

- Dilation factor, dimensionless.

If we know that
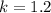k = 1.2 , then the area formula for the dilated triangle is:

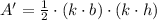
$A' = (1)/(2)\cdot (k\cdot b)\cdot (k\cdot h)$

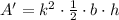
$A' = k^(2)\cdot (1)/(2)\cdot b\cdot h$

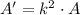
$A' = k^(2)\cdot A$

Therefore, the area of triangle M is 1.44 times the area of triangle M.