Answer:
The answer is "
 "
"
Explanation:
Please find the image file of the angle in the attachment.
Each line is 180° straight because the
 -axis of the 40° and 50° angles is a straight line:
-axis of the 40° and 50° angles is a straight line:

Use this formula and isolate x.
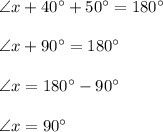
Since the two are vertical angles, they have the same measurement. These have the same measurement. If
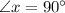 and
and
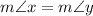 , then
, then
