Answer:
Numbers are 5 , 7
Explanation:
Forming quadratic equation and solving:
Let the two consecutive odd numbers be (2x + 1) and (2x + 3)
Their product = 35
(2x + 1)(2x + 3) = 35
Use FOIL method.
2x*2x + 2x*3 + 1*2x + 1*3 = 35
4x² + 6x + 2x + 3 = 35
Combine like terms
4x² + 8x + 3 = 35
4x² + 8x + 3 - 35 = 0
4x² + 8x - 32 = 0
Quadratic equation: 4x² + 8x - 32 = 0
Solving:
4x² + 8x - 32 = 0
Divide the entire equation by 2
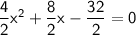
2x² + 4x - 16 = 0
Sum = 4
Product = -32
Factors = 8 , (-4)
When we multiply 8*(-4) = -32 and when we add 8 + (-4) = 4.
Rewrite the middle term
2x² + 8x - 4x - 16 = 0
2x(x + 4) - 4(x + 4) = 0
(x + 4) (2x - 4) = 0
2x - 4 = 0 {Ignore x +4 = 0 as it gives negative number}
2x = 4
x = 4/2
x= 2
2x + 1 = 2*2 + 1 = 5
2x + 3 = 2*2 +3 = 7
The numbers are 5 , 7