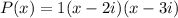Question

Which polynomial function has a leading coefficient of 1 and roots 2i and 3i with multiplicity 1? f(x) = (x – 2i)(x – 3i) f(x) = (x + 2i)(x + 3i) f(x) = (x – 2)(x – 3)(x – 2i)(x – 3i) f(x) = (x + 2i)(x + 3i)(x – 2i)(x – 3i)

Answer 1

a

Explanation:

edge

Answer 2

`P(x)=(x-2i)(x-3i)`

Explanation:

Build a Polynomial Knowing its Roots

If we know a polynomial has roots x1, x2, ..., xn, then it can be expressed as:

`P(x)=a(x-x1)(x-x2)...(x-xn)`

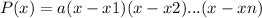
Where a is the leading coefficient.

Note the roots appear with their signs changed in the polynomial.

If the polynomial has a leading coefficient of 1 and roots 2i and 3i with multiplicity 1, then:

`P(x)=1(x-2i)(x-3i)`

`\mathbf{P(x)=(x-2i)(x-3i)}`