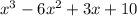Answer:
a) factors of polynomial are: (x+1)(x-2)(x-5)
b) the required polynomial in standard form is:
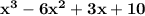
Explanation:
The polynomial has zeros at -1,2,5
Part A) Write the three factors of the polynomial
we have x=-1, x=2 and x=5 as zeros of polynomial
so factors will be:
(x+1)=0, (x-2)=0, (x-5)=0
So, factors of polynomial are: (x+1)(x-2)(x-5)
Part B) Write the polynomial in standard form
For finding polynomial, we will multiply all the factors i.e
(x+1)(x-2)(x-5)
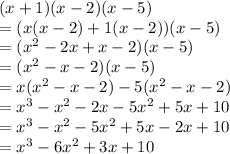
So, the required polynomial in standard form is: