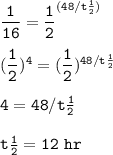Question

After decaying for 48 hours, one-sixteenth (1/16) of the original mass of a radioisotope sample remains unchanged. What is the half-life of this radioisotope?

Answer 1

The half-life of this radioisotope : 12 hr

Further explanation

The atomic nucleus can experience decay into 2 particles or more due to the instability of its atomic nucleus.

Usually radioactive elements have an unstable atomic nucleus.

General formulas used in decay:

`\large{\boxed{\bold{N_t=N_0((1)/(2))^{t/t(1)/(2) }}}`

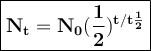
t = duration of decay

t 1/2 = half-life

N₀ = the number of initial radioactive atoms

Nt = the number of radioactive atoms left after decaying during T time

t=48 hr

`\tt (Nt)/(No)=(1)/(16)`

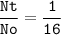
The half-life :

`\tt (1)/(16)=(1)/(2)^{(48/t(1)/(2) )}\\\\((1)/(2))^4=((1)/(2))^{48/t(1)/(2)}\\\\4=48/t(1)/(2)\\\\t(1)/(2)=12~hr`