Question

Are these lines parallel, perpendicular, or neither? 3y=x+4 and 3x+y=1

Answer 1

perpendicular

Explanation:

3y = x + 4 in slope intercept form y = 1/3x +4/3

3x + y = 1 in slope intercept form y = -3x +1

the slopes are negative reciprocals of each other so they are perpendicular

Answer 2

These lines are perpendicular

Explanation:

3y=x+4

`y = (1)/(3)x+(4)/(3)`

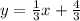
Slope (m1) = 1/3

3x+y=1

y = -3x + 1

Slope (m2) = - 3

m1 * m2 =
`(1)/(3)* -3`

= -1

So, these lines are perpendicular.

If product of two slopes is (-1), then they are perpendicular lines.

If both lines have same slope, then they are parallel.