Answer:
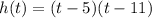
The swimmer comes back up 11 seconds after the timer is started.
The swimmer dives into the water 5 seconds after the timer is started.
Explanation:
Given function:
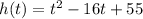
To factor a quadratic in the form
 ,
,
find two numbers that multiply to
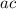 and sum to
and sum to
 :
:
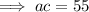

Two numbers that multiply to 55 and sum to -16 are: -11 and -5
Rewrite b as the sum of these two numbers:
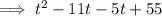
Factorize the first two terms and the last two terms separately:
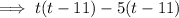
Factor out the common term (t - 11):
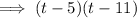
Therefore, the given formula in factored form is:
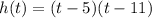
The swimmer's depth is modeled as h(t). Therefore, when h(t) = 0 the swimmer will be at the surface of the water.
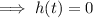
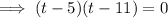

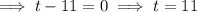
Therefore, the swimmer will be at the surface of the water at 5 s and 11 s.
The swimmer's maximum depth is the vertex of the function. The x-value of the vertex is the midpoint of the zeros. Therefore, the x-value of the vertex is t = 8.
Substitute t = 8 into the function to find the maximum depth:
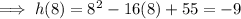
So the swimmer's maximum depth is 9 ft.
True Statements
The swimmer comes back up 11 seconds after the timer is started.
The swimmer dives into the water 5 seconds after the timer is started.