Question

A rectangular solid has width w, a length of 7 more than the width, and a height that is equivalent to 15 decreased by 3 times the width. Express the volume in terms of the width. Then find the maximum volume

Answer 1

For a rectangular solid with:

width = w

length = l

height = h

The volume is equal to:

V = w*l*h

in this case we know that:

width = w.

"length of 7 more than the width"

l = w + 7.

"a height that is equivalent to 15 decreased by 3 times the width."

h = 15 - 3*w

Then the volume will be:

V = w*l*h = w*(w + 7)*(15 - 3w) = (w^2 + 7*w)*(15 - 3*w)

V = ( -3*w^3 + 15*w^2 + 105*w - 21*w^2)

V = (-3*w^3 - 6*w^2 + 105*w)

Now, the maximum volume will be for the value of w such that:

V'(w) = 0.

and:

V''(W) < 0

Where:

dV/dw = V'(w).

dV'/dw = V''(w)

Then first we need to differentiate the equation for the volume.

V'(w) = dV/dw = ( 3*(-3*w^2) + 2*(-6*w) + 105)

V'(w) = -9*w^2 - 12*w + 105.

Then we need to find the solution for:

-9*w^2 - 12*w + 105 = 0.

We can use the Bhaskara formula, and we will get:

`w = (+12 +-√((-12)^2 - 4*(-9)*105) )/(2*-9) = (+12 +- 62.6)/(-18)`

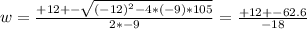
Then the two solutions are:

w₁ = (+12 - 62.6)/(-18) = 2.81

w₂ = (+12 + 62.6)/(-18) = -15.5

But we can not have a negative width, so we can just discard the second solution.

Now let's check the second condition for the maximum, we must have:

V''(2.81) < 0.

V'' = dV'/dw = 2*(-9*w) - 12 = -18*w - 12

V''(2.81) = -18*2.81 - 12 = -62.58 < 0 .

Then the volume is maximized when w = 2.81, and the maximum volume will be:

V(2.81) = (-3*(2.81)^3 - 6*(2.81)^2 + 105*2.81) = 180.1