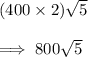Question

I need this answer as soon as possible! 50 points!

Answer 1

`20^(\tfrac 52)\\\\=(20^5)^(\tfrac 12)\\\\=\left(20^4 \cdot 20 \right)^(\tfrac 12)\\\\=20^(\tfrac 42) \cdot 20^(\tfrac 12)\\\\=20^2 √(20)\\\\=400√(4 * 5)\\\\=400 * 2\sqrt 5\\\\=800\sqrt 5`

Answer 2

`800√(5)`

Explanation:

Given:
`\large (20)^\text{$ (5)/(2) $}`

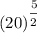
Properties of Exponents:

Rational Exponent Property:
`\large x^\text{$ (m)/(n) $} = \large \text{$ \sqrt[n]{x^m} $}`

• a number raised to a fraction, can be converted to a radical.
• the numerator becomes the exponent, and the denominator becomes the index of the radical.

Product of Powers Property:

• when multiplying powers with the same base, add the exponents.

1. Convert into a radical:

`\sqrt[2]{20^5} \implies √(20^5)`

2. Simplify the expression:

`√(20^2*20^2*20^1)\\\\\implies √(20^4*20)\\\\\implies 20^2√(20)\\\\\implies 20^2√(4*5)\\\\\implies 20^2*2√(5)`

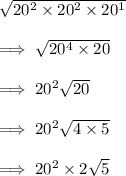
3. Evaluate the power:

`20*20*2√(5)\\\\\implies 400*2√(5)`

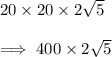
4. Multiply:

`(400*2)√(5)\\\\\implies800√(5)`