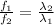Question

One light beam has wavelength, and frequency, fl. Another light beam has wavelength, in, and frequency, f2. Write a proportion that shows how the ratio of the wavelengths of these two light beams is related to the ratio Of their frequencies.

Answer 1

The question is missing. Here is the complete question.

One light beam has wavelength,
`\lambda_(1)`, and frequency, f₁. Another light beam has wavelength,
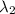`\lambda_(2)`, and frequency, f₂. Write a proportion that shows how the ratio of the wavelengths of these two light beams is related to the ratio of the frequencies.

Answer:
`(f_(1))/(f_(2)) =(\lambda_(2))/(\lambda_(1))`

Step-by-step explanation: In vacuum, eletromagnetic waves travels at a constant speed called "speed of light", whose symbol is [c] and magnitude is 3x10⁸m/s.

Speed of light, frequency and wavelength are related by the formula:

`c=\lambda.f`

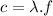
So, if one light beam has wavelength and frequency,
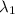`\lambda_(1)` and f₁, respectively, the second beam has wavelength
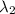`\lambda_(2)` and frequency f₂ and both travel at speed of light:

`\lambda_(1)f_(1)=\lambda_(2)f_(2)`

`(f_(1))/(f_(2))=(\lambda_(2))/(\lambda_(1))`

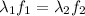
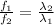
Then, the ratio that shows the relation between frequencies and wavelengths of these light beams is
`(f_(1))/(f_(2))=(\lambda_(2))/(\lambda_(1))`