Question

A gardener is planting two types of trees: Type A is 10 feet tall and grows at a rate of 19 inches per year. Type B is 4 feet tall and grows at a rate of 25 inches per year. Algebraically determine exactly how many years it will take for these trees to be the same height.

Answer 1

It'll take 12 years

Explanation:

Given

Type A:

`Initial\ Height = 10ft`

`Growth = 19in`

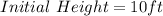
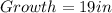
Type B:

`Initial\ Height = 4ft`

`Growth = 25in`

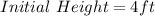
Required

Determine the years they'll reach the same height

First, convert feet to inches in both measurements (this is done by multiplying measurement by 12):

Type A:

`Initial\ Height = 10ft`

`Initial\ Height = 10 * 12in`

`Initial\ Height = 120in`

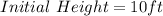
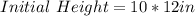
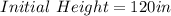
Type B:

`Initial\ Height = 4ft`

`Initial\ Height = 4 * 12in`

`Initial\ Height = 48in`

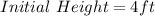
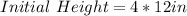
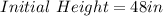
The height at any year from both trees is calculated using

`Height = Iniital\ Height + Growth * x`

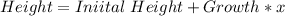
Where x represents the year;

For Type A:

`Height = 120+ 19 * x`

`Height = 120+ 19x`

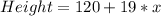
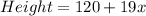
For Type B:

`Height = 48+ 25 * x`

`Height = 48+ 25x`

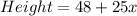
To get when their height will be equal, we simply equate both expressions:

`48+ 25x = 120 + 19x`

Collect Like Terms

`25x - 19x= 120 - 48`

`6x= 72`

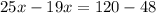
Solve for x

`x = 72/6`

`x = 12`

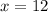
Hence, It'll take 12 years