Answer:
The equation in point-slope form of the line that represents the height of the bucket relative to the top of the well is
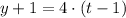 .
.
Explanation:
The point-slope form of the equation of the line is represented by the following expression:
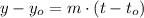 (1)
(1)
Where:
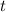 - Time, measured in seconds.
- Time, measured in seconds.
 - Height below the top of the well, measured in feet.
- Height below the top of the well, measured in feet.
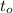 ,
,
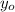 - Known information of the well, measured in seconds and feet, respectively.
- Known information of the well, measured in seconds and feet, respectively.
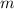 - Slope, measured in feet per second.
- Slope, measured in feet per second.
If we know that
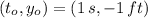 and
and
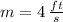 , then the equation in point-slope form of the line is:
, then the equation in point-slope form of the line is:
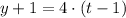
The equation in point-slope form of the line that represents the height of the bucket relative to the top of the well is
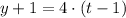 .
.