Answer:
a) El trabajo realizado por esta fuerza mientras el bloque se mueve desde la posición x = + 10 m hasta la posición x = + 20 m es 900 joules.
b) La rapidez del bloque en la posición x = + 20 metros es aproximadamente 5.701 metros por segundo.
Step-by-step explanation:
a) El trabajo expermentado por el bloque (
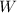 ), medido en joules, es definida por la siguiente ecuación integral:
), medido en joules, es definida por la siguiente ecuación integral:
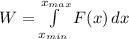 (1)
(1)
Donde:
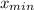 ,
,
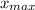 - Posiciones mínima y máxima del bloque, medidos en metros.
- Posiciones mínima y máxima del bloque, medidos en metros.
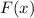 - Fuerza horizontal aplicada al bloque, medida en newtons.
- Fuerza horizontal aplicada al bloque, medida en newtons.
Si conocemos que
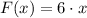 ,
,
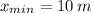 y
y
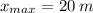 , entonces el trabajo realizado por esta fuerza es:
, entonces el trabajo realizado por esta fuerza es:
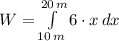 (2)
(2)
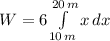
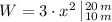
![W = 3\cdot [(20\,m)^(2)-(10\,m)^(2)]](https://img.qammunity.org/2021/formulas/physics/high-school/ofr10v1rec34h9n172wjpa3699k0d43azb.png)
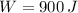
El trabajo realizado por esta fuerza mientras el bloque se mueve desde la posición x = + 10 m hasta la posición x = + 20 m es 900 joules.
b) La rapidez final del bloque se determina mediante de Teorema del Trabajo y la Energía, es decir:
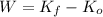 (3)
(3)
Donde son
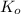 ,
,
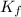 las energías cinéticas traslacionales inicial y final, medidos en joules.
las energías cinéticas traslacionales inicial y final, medidos en joules.
Al aplicar la definición de energía cinética traslacional, expandimos y simplificamos la ecuación como sigue:
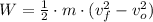 (4)
(4)
Donde:
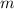 - Masa del bloque, medido en kilogramos.
- Masa del bloque, medido en kilogramos.
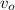 ,
,
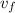 - Rapideces inicial y final del bloque, medidos en metros por segundo.
- Rapideces inicial y final del bloque, medidos en metros por segundo.
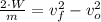
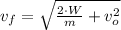
Si conocemos que
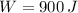 ,
,
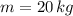 y
y
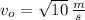 , entonces la rapidez final del bloque es:
, entonces la rapidez final del bloque es:

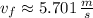
La rapidez del bloque en la posición x = + 20 metros es aproximadamente 5.701 metros por segundo.