Question

Complete the table of values for this absolute value function. Then use the drawing tool(s) to graph the function. F(x)-2|x+1|-1

Answer 1

Please check the explanation!

Explanation:

Given the equation

`f\left(x\right)=-2|x+1|-1`

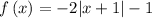
As some of the absolute rules are:

• 
  `\left|a\right|=a,\:a\ge 0`

• 
  `\:|-a|=a,\:\quad \:a>0`

NOW, let us solve!

Let us substitute all the table values

Putting x = -4

`y=-2\left|-4+1\right|-1` ∵
`\mathrm{Apply\:absolute\:rule}:\quad \left|a\right|=a,\:a\ge 0`

`y=-6-1`

`y=-7`

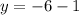
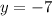
So, when x = -4, then y = -7

Putting x = -3

`y=-2|-3+1|-1\:`

`y=-4-1`

`y=-5`

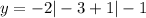
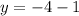
when x = -3, then y = -5

Putting x = -2

`y=-2\left|-2+1\right|-1`

`y=-2-1`

`y=-3`

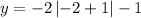
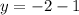
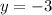
when x = -2, then y = -3

Putting x = -1

`y=-2\left|-1+1\right|-1`

`y=-0-1`

`y=-1`

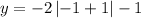
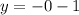
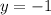
when x = -1, then y = -1

Putting x = 0

`y=-2\left|0+1\right|-1`

`y=-2-1`

`y=-3`

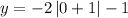
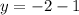
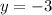
when x = 0, then y = -3

Putting x = 1

`y=-2\left|1+1\right|-1`

`y=-4-1`

`y=-5`

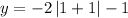
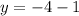
when x = 1, then y = -5

The graph is also attached below.