Question

Find the Derivative.
f(x) = -xcos3x

Answer 1

Hi there!

`\large\boxed{f'(x) = -cos3x + 3xsin3x}`

`f(x) = -xcox3x\\\\\text{Use the product rule and chain rule to solve for the derivative:}\\\\(dy)/(dx)= -cos3x + (-x * (-sin3x) * 3)\\\\= -cos3x + 3xsin3x`

Answer 2

`(d)/(dx)(-xcos3x)= 3x \ sin(3x)- cos(3x)`

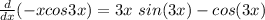
Explanation:

Use the Product Rule for derivatives, which states that:

• 
  `(d)/(dx) =[f(x)g(x)]= f(x)g'(x)+f'(x)g(x)`

In the function we are given,
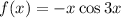`f(x)=-x \cos3x`, we can break it up into two factors: -x is being multiplied by cos3x.

Now, we have the factors:

• 
  `-x \\ $cos 3x`

Before using the product rule, let's find the derivative of cos3x using the chain rule and the power rule.

• 
  `(d)/(dx)(cos3x)= (d)/(dx) (cos3x) * (d)/(dx) (3x) \\ (d)/(dx)(cos3x)= (-sin3x) * 3 \\ (d)/(dx) (cos3x) = -3sin(3x)`

Now let's apply the product rule to f(x) = -xcos3x.

• 
  `(d)/(dx)(-xcos3x)= (-x)(-3sin3x) + (-1)(cos3x)`

Simplify this equation.

• 
  `(d)/(dx)(-xcos3x)= (x)(3sin3x) - (cos3x)`

Multiply x and 3 together and remove the parentheses.

• 
  `(d)/(dx)(-xcos3x)= 3x \ sin(3x)- cos(3x)`

Therefore, this is the derivative of the function
`f(x)=-xcos3x`.