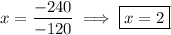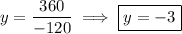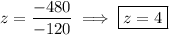Question

Use Cramer’s rule to solve for x: x + 4y − z = −14 5x + 6y + 3z = 4 −2x + 7y + 2z = −17

Answer 1

Looks like the system is

x + 4y - z = -14

5x + 6y + 3z = 4

-2x + 7y + 2z = -17

or in matrix form,

`\mathbf{Ax} = \mathbf b \iff \begin{bmatrix} 1 & 4 & -1 \\ 5 & 6 & 3 \\ -2 & 7 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -14 \\ 4 \\ -17 \end{bmatrix}`

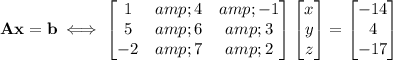
Cramer's rule says that

`x_i = (\det \mathbf A_i)/(\det \mathbf A)`

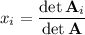
where
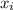`x_i` is the solution for i-th variable, and
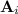`\mathbf A_i` is a modified version of
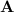`\mathbf A` with its i-th column replaced by
`\mathbf b`.

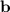We have 4 determinants to compute. I'll show the work for det(A) using a cofactor expansion along the first row.

`\det \mathbf A = \begin{vmatrix} 1 & 4 & -1 \\ 5 & 6 & 3 \\ -2 & 7 & 2 \end{vmatrix}`

`\det \mathbf A = \begin{vmatrix} 6 & 3 \\ 7 & 2 \end{vmatrix} - 4 \begin{vmatrix} 5 & 3 \\ -2 & 2 \end{vmatrix} - \begin{vmatrix} 5 & 6 \\ -2 & 7 \end{vmatrix}`

`\det \mathbf A = ((6*2)-(3*7)) - 4((5*2)-(3*(-2)) - ((5*7)-(6*(-2)))`

`\det\mathbf A = 12 - 21 - 40 - 24 - 35 - 12 = -120`

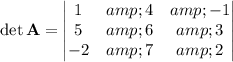
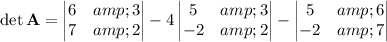
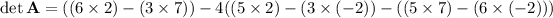
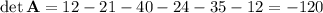
The modified matrices and their determinants are

`\mathbf A_1 = \begin{bmatrix} -14 & 4 & -1 \\ 4 & 6 & 3 \\ -17 & 7 & 2\end{bmatrix} \implies \det\mathbf A_1 = -240`

`\mathbf A_2 = \begin{bmatrix} 1 & -14 & -1 \\ 5 & 4 & 3 \\ -2 & -17 & 2 \end{bmatrix} \implies \det\mathbf A_2 = 360`

`\mathbf A_3 = \begin{bmatrix} 1 & 4 & -14 \\ 5 & 6 & 4 \\ -2 & 7 & -17 \end{bmatrix} \implies \det\mathbf A_3 = -480`

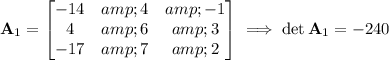
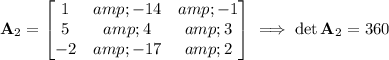
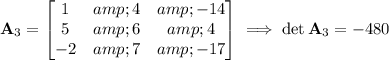
Then by Cramer's rule, the solution to the system is

`x = (-240)/(-120) \implies \boxed{x = 2}`

`y = (360)/(-120) \implies \boxed{y = -3}`

`z = (-480)/(-120) \implies \boxed{z = 4}`

Answer 2

in photo attached.

Explanation: