Question

A ball is thrown straight up into the air from the top of a building standing at 50 feet with an initial velocity of 65 feet per second the height of the ball in feet can be modeled by the following function: h(t)=-16t^2++16t+96 When does the ball reach its maximum height?

Answer 1

0.5 seconds (at 100 feet in the air).

Explanation:

So, the height of the ball can be modeled by the function:

`h(t)=-16t^2+16t+96`

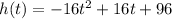
Where h(t) represents the height in feet after t seconds.

And we want to find its maximum height.

Notice that our function is a quadratic.

Therefore, the maximum height will occur at the vertex of our function.

The vertex of a quadratic function in standard form is given by the formula:

`(-(b)/(2a), f(-(b)/(2a)))`

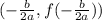
In our function, a=-16; b=16; and c=96.

Find the x-coordinate of the vertex:

`x=-((16))/(2(-16))=1/2`

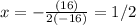
So, the ball reaches its maximum height after 0.5 seconds of its projection.

Notes:

To find it’s maximum height, we can substitute 1/2 for our function and evaluate. So:

`h(1/2)=-16(1/2)^2+16(1/2)+96`

Evaluate:

`h(1/2)=-4+8+96=100`

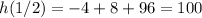
So, the ball reaches its maximum height of 100 feet 0.5 seconds after its projection.