Answer:
The student must change the launch angle from 20º to 45º to maximize the horizontal distance.
Step-by-step explanation:
The dart experiments a parabolical motion, which is the combination of horizontal uniform motion and vertical uniform accelerated motion due to gravity, in which effects from air friction and Earth's rotation can be neglected. The equations of motion are described below:
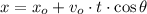 (1)
(1)
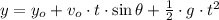 (2)
(2)
Where:
 ,
,
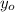 - Initial coordinates of the dart, measured in meters.
- Initial coordinates of the dart, measured in meters.
 ,
,
 - Current coordinates of the dart, measured in meters.
- Current coordinates of the dart, measured in meters.
 - Initial velocity of the dart, measured in meters per second.
- Initial velocity of the dart, measured in meters per second.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
 - Launch angle, measured in sexagesimal degrees.
- Launch angle, measured in sexagesimal degrees.
According to the statement, we need to determine the launch angle when
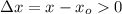 ,
,
 and
and
 . Then, we obtain the following system of linear equations:
. Then, we obtain the following system of linear equations:
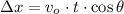 (1b)
(1b)
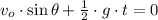 (2b)
(2b)
By (2b), we clear time as follows:
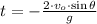
And it is applied in (1b) afterwards:
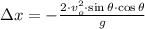
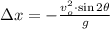 (3)
(3)
Where
 is the horizontal distance, measured in meters.
is the horizontal distance, measured in meters.
In order to determine the launch angle such that distance is maximized, we require the first and second derivatives of the function. That is:
First derivative
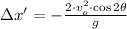 (4)
(4)
Second derivative
 (5)
(5)
By equalizing (4) to zero, we find the following trigonometric equivalence:
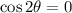
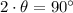
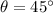
A launch angle of 45º is a critical point of (3). If we know that
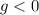 and
and
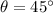 in (5), then
in (5), then
 , which means that critical point determined above leads to a maximum distance. Then, the student must change the launch angle from 20º to 45º to maximize the horizontal distance.
, which means that critical point determined above leads to a maximum distance. Then, the student must change the launch angle from 20º to 45º to maximize the horizontal distance.