Answer:
(10x^4–4x^3+14x^2–14x–16)/(2x–2) =
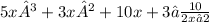
Step-by-step explanation:
Given the quotient of two polynomials, you can use synthetic division to quickly divide the two.
First find the root of the denominator.
2x - 2 → 2x - 2 = 0 → 2x = 2 → x = 1.
Now since the denominator has a greatest common factor of 2 because 2x -2 = 2(x-1) this is what we will divide the result by at the end.
Synthetic division is a quicker method relative to polynomial long division.
It is in the format of:
R(Root of denominator) | a b. c .........
+aR +R(b+aR)...
|__________
a b+aR c + R(b+aR) .... ..
Since the denominator has a degree of 1
The results on the bottom are the coefficients of the divided polynomial minus 1 degree respectively.
The letters are the coefficients of the polynomial from a → z.
For this particular expression of two polynomials that are being divided.
Here is it's format in synthetic division:
The coefficient of the highest term is an exception and is just dropped down.
(10x^4-4x^3+14x^2-14x-16)/(2x-2)
= 1 | (10) (-4) (14) (-14) (-16)
↓ +10 +6 +20. +6
↓ ↓ ↓ ↓
|___________
10 6 20 6 -10