Explanation:
Remember that
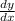
is the gradient or slope function.
So we need to analyze the slope of each graph over given time.l and how it changes.
For the 1st graph, we have a linear function.
Remember the special properties for all linear functions:
The slope at any two points on the line is the same.
So this means our slope here must be constant.
And since our slope is negative, our dy/dx, function must be a constant function that is negative. So
The answer for the first graph is draw a horizontal line underneath the x axis.
For the 2nd graph, we have a slope that is decreasing, reaches 0 at the minimum, then increases even more.
We can draw a linear function that is increasing forever for our dy/dx.
For the 3rd graph, we are increasing , till we hit 0, then decrease until we hit 0, then forever increases.
Our dy/dx will be a parabola that passes through the x axis twice at two different points, facing upwards.
The first , second, and third graph is the dy/dx graphs shown respectively.
All these are examples of possible graphs. If you need more clarification, let me know