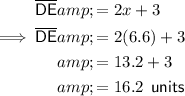Answer:
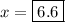
Explanation:
Geometric Mean Theorem - Altitude Rule
The altitude drawn from the vertex of the right angle perpendicular to the hypotenuse separates the hypotenuse into two segments. The ratio of one segment to the altitude is equal to the ratio of the altitude to the other segment:
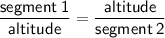
From inspection of the given diagram:
- altitude = FD = 9
- segment 1 = CD = 5
- segment 2 = DE =
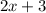
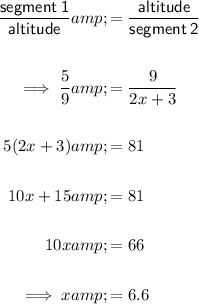
Substitute the found value of x into the expression for DE: