Answer:
1000 dollars
Explanation:
Given
P: ---2 -----,4 ----,6
C: 1200, 1400, 1600
Required
Calculate the fixed cost
First, we need to determine the equation that determines the relationship between P and C
We start by selecting any two corresponding values of P and C
We have that:
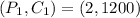
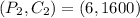
Calculate the slope, using:
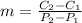
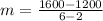
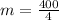
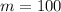
The equation is then calculated using:
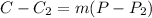
Where
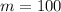 and
and
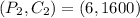
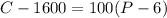
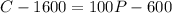
Collect Like Terms
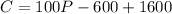
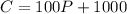
From the equation above,
100P represents the amount paid for P phones produced
1000 represents the fixed cost paid
C represents the total amount paid