BC is not 2 units long; CA is not 5 units long; BC is shorter than BA; AC is not 2 units longer than BC.
- No. The length of BC can be found using the distance formula:
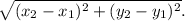
![\[BC = √(((-1) - (-1))^2 + (1 - 4)^2) = √(0^2 + 3^2) = 3 \text{ units}\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/uwrm283dchxpay01hbq0a5rqhhiwb2mamn.png)
- No. Similarly, using the distance formula for CA:
![\[CA = √((4 - (-1))^2 + (1 - 1)^2) = √(5^2 + 0^2) = 5 \text{ units}\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/exk1ztinf6fnyxu1kg2o5kcvbo0j177jeg.png)
- Yes. Comparing the lengths using the distance formula:
![\[BA = √(((-1) - 4)^2 + (4 - 1)^2) = √((-5)^2 + 3^2) = √(25 + 9) = √(34) \text{ units}\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/recseg61qpx72xm0hhq79bnrqvdvtrnv3n.png)
BC is 3 units, which is shorter than
 .
.
- AC is 2 units longer than BC.
- No. The length of AC is 5 units, while BC is 3 units. The difference is
 units, so AC is not 2 units longer than BC.
units, so AC is not 2 units longer than BC.