Answer:
Perpendicular
Explanation:
Given
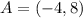



Required
Is AB and CD parallel?
First, we need to calculate the slope (m) of AB and CD

For AB:
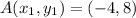

So:

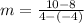
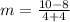

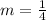
For CD:

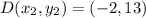
So:

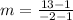
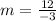
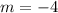
For Lines to be parallel, the slope must be equal:
i.e.
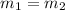
This condition is not true because:
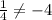
For Lines to be perpendicular, the slope must be:

This implies:

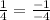

Hence, the lines are perpendicular