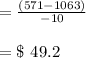Question

Let C(t) be the amount of U.S. cash per capita in circulation at time 1. The table, supplied by the Treasury Department, gives values of C(t) as of June 30 of the specificd year. Interpret and estimate the value of C'(1980).

Answer 1

Following are the solution to this question:

Explanation:

C'(t) was its time, in years, or t shift of cash per unit. That C'(1980) meaning, therefore, becomes the change of cashier's population to t = 1980.

They could either use t = 1970 or t = 1990 to approximate the C'(1980) price. When using t = 1970:

`C'(1980) = ([C(1980) - C(1970)])/([1980 - 1970])\\\\`

`= ((571 - 265))/(10)\\\\ = \$ \ 30.6 \\`

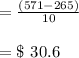
t = 1990:

`C'(1980) = ([C(1980) - C(1990)])/([1980 - 1990])`

`= ((571 - 1063))/( -10) \\\\= \$ \ 49.2`