Question

Find the limit of the formula given​

Answer 1

`\displaystyle \lim_(x \to 0^+) x^\big{√(x)} = 1`

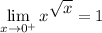
General Formulas and Concepts:

Algebra II

• Natural logarithms ln and Euler's number e
• Logarithmic Property [Exponential]:
  `\displaystyle log(a^b) = b \cdot log(a)`

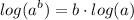
Calculus

Limits

• Right-Side Limit:
  `\displaystyle \lim_(x \to c^+) f(x)`
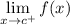
• Left-Side Limit:
  `\displaystyle \lim_(x \to c^-) f(x)`

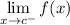
Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

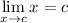
L’Hopital’s Rule:
`\displaystyle \lim_(x \to c) (f(x))/(g(x)) = \lim_(x \to c) (f'(x))/(g'(x))`

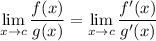
Differentiation

• Derivatives
• Derivative Notation

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Explanation:

We are given the following limit:

`\displaystyle \lim_(x \to 0^+) x^\big{√(x)}`

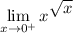
Substituting in x = 0 using the limit rule, we have an indeterminate form:

`\displaystyle \lim_(x \to 0^+) x^\big{√(x)} = 0^0`

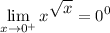
We need to rewrite this indeterminate form to another form to use L'Hopital's Rule. Let's set our limit as a function:

`\displaystyle y = \lim_(x \to 0^+) x^\big{√(x)}`

Take the ln of both sides:

`\displaystyle lny = ln \Big( \lim_(x \to 0^+) x^\big{√(x)} \Big)`

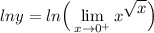
Rewrite the limit by including the ln in the inside:

`\displaystyle lny = \lim_(x \to 0^+) ln \big( x^\big{√(x)} \big)`

Rewrite the limit once more using logarithmic properties:

`\displaystyle lny = \lim_(x \to 0^+) √(x)ln(x)`

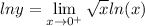
Rewrite the limit again:

`\displaystyle lny = \lim_(x \to 0^+) (ln(x))/((1)/(√(x)))`

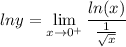
Substitute in x = 0 again using the limit rule, we have an indeterminate form in which we can use L'Hopital's Rule:

`\displaystyle \lim_(x \to 0^+) (ln(x))/((1)/(√(x))) = (\infty)/(\infty)`

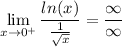
Apply L'Hopital's Rule:

`\displaystyle \lim_(x \to 0^+) (ln(x))/((1)/(√(x))) = \lim_(x \to 0^+) \frac{(1)/(x)}{\frac{-1}{2x^\big{(3)/(2)}}}`

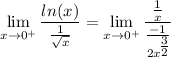
Simplify:

`\displaystyle \lim_(x \to 0^+) \frac{(1)/(x)}{\frac{-1}{2x^\big{(3)/(2)}}} = \lim_(x \to 0^+) -2√(x)`

Redefine the limit:

`\displaystyle lny = \lim_(x \to 0^+) -2√(x)`

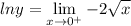
Substitute in x = 0 once more using the limit rule:

`\displaystyle \lim_(x \to 0^+) -2√(x) = -2√(0)`

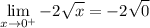
Evaluating it, we have:

`\displaystyle \lim_(x \to 0^+) -2√(x) = 0`

Substitute in the limit value:

`\displaystyle lny = 0`

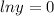
e both sides:

`\displaystyle e^\big{lny} = e^\big{0}`

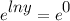
Simplify:

`\displaystyle y = 1`

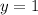
And we have our final answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits