Answer:
The speed of the apple will be 2.81 m/s when the arrow enters it.
Step-by-step explanation:
We can find the speed of the apple by conservation of linear momentum:
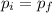
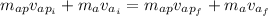
Where:
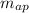 is the mass of the apple = 100 g = 0.1 kg
is the mass of the apple = 100 g = 0.1 kg
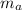 is the mass of the arrow = 2.5 g = 0.0025 kg
is the mass of the arrow = 2.5 g = 0.0025 kg
 and
and
 is the initial and final speed of the apple respectively
is the initial and final speed of the apple respectively
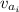 and
and
 is the initial and final speed of the arrow respectively
is the initial and final speed of the arrow respectively
Since the apple was originally at rest (
 = 0) and knowing that
= 0) and knowing that
 =
=
 when the arrow enters into the apple, we have:
when the arrow enters into the apple, we have:
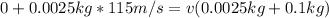
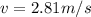
Therefore, the speed of the apple will be 2.81 m/s when the arrow enters it.
I hope it helps you!