Answer:
A rational number is a number that can be expressed as a fraction (the ratio of two integers).
Integer: A whole number that can be positive, negative, or zero.
To calculate if each radical can be expressed as a rational number, convert the decimals into rational numbers, then simplify:
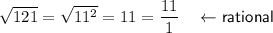
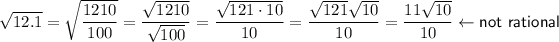
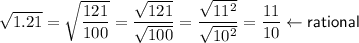
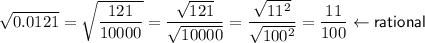
Therefore,
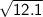 is not a rational number.
is not a rational number.