The missing statement and reason in the table is given below:
Statement Reason
1. ∠ABD ≅ ∠CDB; ∠ADB ≅ ∠CBD
Opposite angles in a parallelogram are congruent.
2. ΔABD ≅ ΔCDB
Side-Angle-Side (SAS) postulate of congruence. |
3. AB ≅ CD and BC ≅ AD
Corresponding parts of congruent triangles are congruent (CPCTC).
1. In a parallelogram, opposite sides are parallel by definition. Therefore, angle
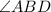 is congruent to angle
is congruent to angle
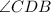 and angle
and angle
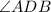 is congruent to angle
is congruent to angle
 because they are alternate interior angles formed by a transversal with two parallel lines.
because they are alternate interior angles formed by a transversal with two parallel lines.
2. We also know that side
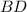 is shared between triangles
is shared between triangles
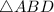 and
and
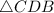 , so it is congruent to itself by the reflexive property of equality.
, so it is congruent to itself by the reflexive property of equality.
3. With two angles and the side between them congruent (SAS), we can say that
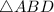 is congruent to
is congruent to
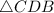 .
.
4. Because the triangles are congruent, all corresponding parts are congruent. Therefore, side
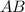 is congruent to side
is congruent to side
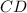 , and side
, and side
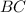 is congruent to side
is congruent to side
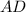 , by CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
, by CPCTC (Corresponding Parts of Congruent Triangles are Congruent).