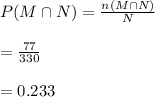Question

Statistics Probability

A survey of a freshmen English class asked students whether or not they ate breakfast the morning of the survey. The results are included in the table to the right.

(a) What is the probability that a randomly selected student ate breakfast?

(b) Of all students, what is the probability that a randomly selected student is female and ate breakfast?

(c) What is the probability a randomly selected student is male, given that the student ate breakfast?

(d) What is the probability that a randomly selected student ate breakfast, given that the student is male?

(e) What is probability of "is male" or "did not eat breakfast"?

(f) What is the probability of "is male and did not eat breakfast?

Answer 1

Explained below.

Explanation:

Denote the variable as follows:

M = male student

F = female student

Y = ate breakfast

N = did not ate breakfast

(a)

Compute the probability that a randomly selected student ate breakfast as follows:

`P(Y)=(n(Y))/(N)\\\\=(198)/(330)\\\\=0.60`

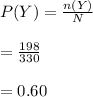
(b)

Compute the probability that a randomly selected student is female and ate breakfast as follows:

`P(F\cap Y)=(n(F\cap Y))/(N)\\\\=(121)/(330)\\\\=0.367`

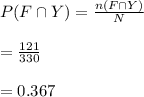
(c)

Compute the probability a randomly selected student is male, given that the student ate breakfast as follows:

`P(M|Y)=(n(M\cap Y))/(n(Y))\\\\=(77)/(198)\\\\=0.389`

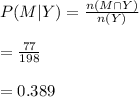
(d)

Compute the probability that a randomly selected student ate breakfast, given that the student is male as follows:

`P(Y|M)=(n(Y\cap M))/(n(M))\\\\=(77)/(154)\\\\=0.50`

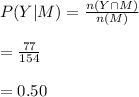
(e)

Compute probability of the student selected "is male" or "did not eat breakfast" as follows:

`P(M\cup N)=P(M)+P(N)-P(M\cap N)\\\\=(n(M))/(N)+(n(N))/(N)-(n(M\cap N))/(N)\\\\=(n(M)-n(N)-n(M\cap N))/(N)\\\\=(154+132-77)/(330)\\\\=0.633`

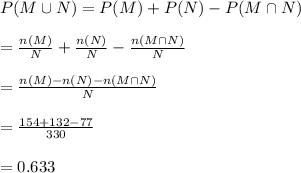
(f)

Compute the probability of "is male and did not eat breakfast as follows:

`P(M\cap N)=(n(M\cap N))/(N)\\\\=(77)/(330)\\\\=0.233`