Given:
Height of access ramp = 6 foot
Ramp ends at a point 40 feet away along the ground.
To find:
The angle of depression in nearest tenth of a degree.
Solution:
Using the given information, draw a figure as shown below.
In a right angle triangle,
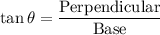
In triangle ABC,
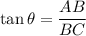
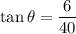

Taking tan inverse on both sides.
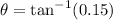
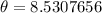
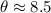
Therefore, the angle of depression is 8.5 degrees.