Question

HELP PLS❗️ Given A(- 1, 4) , B(1, 5) , C(- 5, 3) which coordinate will make line AB parallel to CO?

A, D(-3,4)
B, D(-6,1)
C, D(-7,4)
D, D(-4,5)

Answer 1

The coordinate of the point that will make AB parallel to CO is D(-3, 4)

Explanation:

The given points on the line AB are;

A(-1, 4), and B(1, 5)

The following is the equation for finding the slope of a line given the coordinate of the points

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

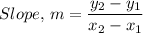
The slope, m, of the segment with points A and B is therefore;

`Slope, \, of \ line \ AB \ m_((AB))=(5-4)/(1-(-1)) = (1)/(2)`

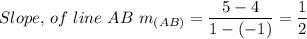
For the line CO to be parallel to the line AB, the slope of line CO must be equal to the slope of the line AB

Therefore, the slope of the line CO = 1/2

The equation of the line CO in point slope form is therefore, y - 3 = 1/2(x - (-5))

y = x/2 + 5/2 + 3

y = x/2 + 11/2

From the given points, the point that satisfies the above equation for the line CO is the point (-3, 4)

y = (-3)/2 + 11/2 = -1.5 + 5.5 = 4

y = 4 when x = -3

Therefore;

The coordinate of the point that will make AB parallel to CO is D(-3, 4).