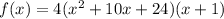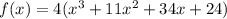Question

Write the cubic polynomial function f(x)in expanded form with zeros −6, −4,and −1,given that f(−2)=−32.

Answer 1

`f(x)=4x^3+44x^2+136x+96`

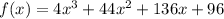
Explanation:

Polynomials

It's possible to build a polynomial function by knowing its zeros and leading coefficient.

Given the zeros of a third-degree polynomial: x=x1, x=x2, and x=x3, the function is:

`f(x)=a(x-x_1)(x-x_2)(x-x_3)`

Where a is the leading coefficient.

We are given the zeros -6, -4, and -1, thus:

`f(x)=a(x+6)(x+4)(x+1)`

The value of a can be calculated by substituting the point (-2,-32):

`a(-2+6)(-2+4)(-2+1)=-32`

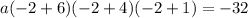
Calculating:

`a(4)(2)(-1)=-32`

`-8a=-32`

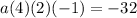
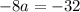
Dividing by -8:

`a = -32/(-8) =4`

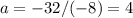
a = 4.

The polynomial is now complete:

`f(x)=4(x+6)(x+4)(x+1)`

Operating:

`f(x)=4(x^2+10x+24)(x+1)`

`f(x)=4(x^3+11x^2+34x+24)`

`\mathbf{f(x)=4x^3+44x^2+136x+96}`