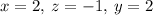Answer:
The solutions to the system of the equations by the elimination method will be:
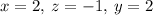
Explanation:
Given the system of the equations
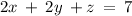
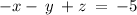
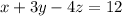
solving the system of the equations by the elimination method
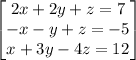
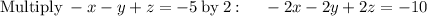
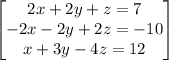
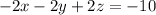

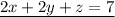

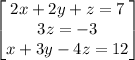


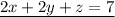
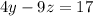
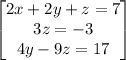
Rearranging the equations
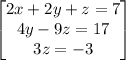
solve
 for z:
for z:

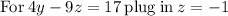
solve
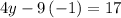 for y:
for y:
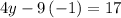
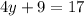
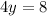
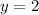
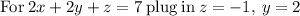
solve
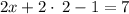 for x:
for x:
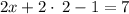
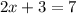
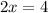
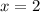
Therefore, the solutions to the system of the equations by the elimination method will be: