Question

Which rational exponent represents a square root?

A. 1 / 2
B. 3/2
C. 1/3
D. 1/4

Answer 1

1/2 rational exponent represents a square root.

Therefore, option A is correct.

Explanation:

As we know that raising to the one-half power i.e.
`(1)/(2)` is the same

as taking the square root.

• so
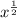  `x^{(1)/(2)}` is the same as the square root of
  `x`.

For example, taking the square root of 4 will determine:

`4^{(1)/(2)}`

`\mathrm{Factor\:the\:number:\:}\:4=2^2`

`4^{(1)/(2)}=\left(2^2\right)^{(1)/(2)}`

`\mathrm{Apply\:exponent\:rule}:\quad \left(a^b\right)^c=a^(bc),\:\quad \:a\ge 0`

`\left(2^2\right)^{(1)/(2)}=2^{2\cdot (1)/(2)}`

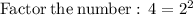
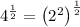
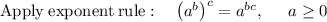
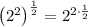
so the expression becomes

`4^{(1)/(2)}=2^{2\cdot \:(1)/(2)}`

`=2^1`

`=2` ∵
`\mathrm{Apply\:exponent\:rule}:\quad \:a^1=a`

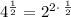
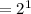
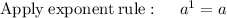
so, 1/2 rational exponent represents a square root.

Therefore, option A is correct.