Answer:
We conclude that option A is true as x = 1 is the root of the polynomial.
Explanation:
Given the polynomial

Let us determine the root of the polynomial shown below.
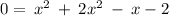
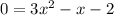
switch sides
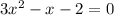
as
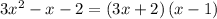
so the equation becomes
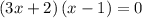
Using the zero factor principle
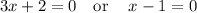
solving
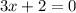
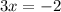
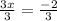
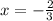
and
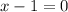

The possible roots of the polynomial will be:
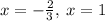
Therefore, from the mentioned options, we conclude that option A is true as x = 1 is the root of the polynomial.